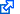I said this many times in my Quora answers, often citing Weinberg: cosmological redshift is due in part to the relativistic Doppler effect, but in large part due to gravitational time dilation. The distant source is not only moving away from us, but it was living in a universe that was much denser than the universe today, hence the average gravitational field was significantly stronger; this means that clocks then, compared to clocks now, would tick slower.
I said this (Weinberg says it) but I never explicitly quantified it. Now is the time to change that.
To do so, let us begin with the standard Friedmann-Lemaître-Robertson-Walker metric:
\begin{align}
ds^2=c^2dt^2-a(t)^2dR^2,\tag{1}
\end{align}
where $a(t)$ is of course the famous scale factor, and $dR$ just refers to the spatial part (e.g., $dR^2=dx^2+dy^2+dz^2$). This is the "comoving" form of the metric, in which the spatial coordinates of things that "go with the flow" remain constant. (This formulation is also what's responsible to the common misunderstanding concerning cosmic expansion: the notion that "space" stretches as opposed to what the equations actually tell us, namely that things are flying apart.)
Let us now rewrite this metric using a redefinition of the spatial coordinate that now incorporates the scale factor: $R'=aR$, i.e., we're no longer using comoving coordinates but rather, a coordinate system of fixed spatial size centered at the observer:
\begin{align}
R’&=aR,\tag{2}\\
dR&=d(a^{-1}R’)=-a^{-2}\dot{a}R’dt+a^{-1}dR’,\tag{3}\\
ds^2&=c^2dt^2-a^2[-a^{-2}\dot{a}R’dt+a^{-1}dR’]^2\\
&=(c^2-a^{-2}\dot{a}^2{R’}^2)dt^2+2a^{-1}\dot{a}R’dtdR’-d{R’}^2\\
&=(c^2-H^2{R’}^2)dt^2+2HR’dtdR’-d{R’}^2, \tag{4}
\end{align}
where we used $H=\dot{a}/a$ as the usual definition of the famous Hubble parameter.
What does this metric tell us? Well, at $R'=0$ (the center) it's just the Minkowski metric. At $R'>0$, however, it tells us that there is a) gravitational time dilation proportional to $\sqrt{1-H^2{R'}^2/c^2}$, and relativistic Doppler corresponding to the velocity $v=HR'$.
In the standard cosmology, we can use the approximation
\begin{align}
\frac{HR'}{c}=\frac{z}{1+z},\tag{5}
\end{align}
where $z$ is the observed redshift of a source at distance $R'$. Using this definition, the gravitational part of the redshift will be
\begin{align}
z_{\rm grav}=\frac{1}{\sqrt{1-\dfrac{H^2{R'}^2}{c^2}}}-1=\frac{1}{\sqrt{1-\dfrac{z^2}{(1+z)^2}}}-1,\tag{6}
\end{align}
whereas the relativistic Doppler due to $v$ is
\begin{align}
z_{\rm Doppler}=\sqrt{\dfrac{c+v}{c-v}}-1=\sqrt{1+2z}-1.\tag{7}
\end{align}
The combined redshift will be the combination of these two contributions:
\begin{align}
z=(1+z_{\rm grav})(1+z_{\rm Doppler})-1,\tag{8}
\end{align}
a result that can be trivially verified using straightforward algebra.
To see the relative contributions in a specific case, let us consider the cosmic microwave background, arriving at a redshift of $1+z\approx 1,100$. The results after substitution are
\begin{align}
z_{\rm grav}&{}\approx 22.46,\tag{9}\\
z_{\rm Doppler}&{}\approx 45.89.\tag{10}
\end{align}
The relationship can also be plotted.
As we can see, the gravitational part (green) becomes significant at high redshift. In contrast, at $z< 1$, the redshift is dominated by Doppler; it takes a while for the gravitational part to "take off":
But given that the Doppler curve remains firmly above the gravitational redshift, why would we imply that the gravitational contribution is dominant? Simple: the contribution is not additive but multiplicative. As we just saw, without gravity, the relativistic Doppler induces a redshift of ~46 at the surface of last scattering. With gravity? The redshift increases to a whopping 1,100.
We must recognize of course that this split into "gravitational time dilation" vs. "Doppler redshift" is dependent on the choice of coordinates. So, how special is the metric (4)? It is not arbitrarily chosen. It is the "natural" metric of an observer at $r=0$ (colocated with the detector), and thus in a very practical sense, accurately represents the split of the redshift into these constituents from that observer's perspective. Indeed, we may recognize (4) as the ADM metric with its shift function in the form of the radial velocity $v=HR'$.